Estadística

La estadística es una rama de las matemáticas que se encarga de recolectar, analizar, interpretar, presentar y organizar datos. La estadística se divide en dos ramas principales:

1. Estadística descriptiva: Se centra en resumir y describir las características de un conjunto de datos. Utiliza medidas como la media, la mediana, la moda, la desviación estándar y la varianza para resumir la información. Además, se utilizan gráficos y tablas para representar visualmente los datos.
2. Estadística inferencial: Se encarga de hacer inferencias y predicciones sobre una población basándose en una muestra de datos. Utiliza técnicas como el muestreo, la estimación de parámetros y las pruebas de hipótesis para hacer estas inferencias. El objetivo es generalizar los resultados de la muestra a toda la población.

Aquí tienes una visión general de los principales conceptos en estadística:

• Población: El conjunto total de elementos o individuos que se estudian.
• Muestra: Un subconjunto de la población que se selecciona para el análisis.
• Variable: Una característica o propiedad que puede variar entre los elementos de la población o muestra. Las variables pueden ser cualitativas (categorías) o cuantitativas (números).
• Distribución de frecuencia: Una tabla que muestra cómo se distribuyen los valores de una variable en la muestra o población.
• Probabilidad: La medida de la certeza o incertidumbre de que ocurra un evento. Es la base para la estadística inferencial.

1. Variables y tipos de variables

Variable: En estadística, una variable es cualquier característica, número o cantidad que puede medirse o contarse. Las variables pueden cambiar y asumir diferentes valores.

Tipos de variables

1. Variables cualitativas (categóricas): Estas variables describen cualidades o categorías. No pueden ser medidas numéricamente de manera significativa.
   • Nominales: Las categorías no tienen un orden específico. Ejemplos: color de ojos, género, tipo de mascota.
   • Ordinales: Las categorías tienen un orden específico, pero las diferencias entre ellas no son cuantificables. Ejemplos: nivel de satisfacción (bajo, medio, alto), clasificación en una competencia (1°, 2°, 3°).
2. Variables cuantitativas (numéricas): Estas variables pueden ser medidas y expresadas numéricamente.
   • Discretas: Pueden asumir un número finito o contable de valores. Ejemplos: número de hijos, cantidad de automóviles.
   • Continuas: Pueden asumir cualquier valor dentro de un intervalo. Ejemplos: altura, peso, temperatura.

Gráficas para tipos de datos

Gráficas para variables cualitativas:

1. Gráfica de barras: Se utiliza para representar frecuencias de categorías en variables cualitativas. Cada barra representa una categoría y su altura representa la frecuencia o porcentaje.
2. Gráfico circular (pastel): Muestra la proporción de cada categoría en un todo. Cada segmento del círculo representa una categoría, y su tamaño es proporcional a su frecuencia o porcentaje.

Gráficas para variables cuantitativas:

1. Histograma: Se utiliza para representar la distribución de variables cuantitativas continuas. Las barras representan intervalos de valores y su altura indica la frecuencia.
2. Diagrama de caja (boxplot): Muestra la mediana, cuartiles y valores atípicos de una variable cuantitativa. Es útil para resumir la distribución y detectar valores atípicos.
3. Gráfica de dispersión (scatter plot): Representa la relación entre dos variables cuantitativas. Cada punto en la gráfica representa una observación con dos valores asociados.

2. Descripción de datos con medidas numéricas

Medidas de centro

1. Media: Es el promedio aritmético de un conjunto de datos. Se calcula sumando todos los valores y dividiéndolos por el número de valores. $$ \text{Media} = \frac{\sum x}{n} $$
   • Ejemplo práctico: La media de las edades de un grupo de personas puede indicarnos la edad promedio del grupo.
2. Mediana: Es el valor central de un conjunto de datos ordenados. Si el número de observaciones es par, la mediana es el promedio de los dos valores centrales.
   • Ejemplo práctico: La mediana del ingreso de un grupo de personas puede ser más representativa que la media, especialmente si hay valores atípicos muy altos o bajos.
3. Moda: Es el valor que más se repite en un conjunto de datos.
   • Ejemplo práctico: La moda en las tallas de zapatos de un grupo de personas nos indica cuál es la talla más común.

Medidas de variabilidad

1. Rango: Es la diferencia entre el valor máximo y el valor mínimo en un conjunto de datos. $$ \text{Rango} = \text{Valor máximo} – \text{Valor mínimo} $$
   • Ejemplo práctico: El rango de las temperaturas en una semana nos da una idea de la amplitud de variación.
2. Varianza: Es la medida de la dispersión de los valores respecto a la media. Se calcula como el promedio de las diferencias al cuadrado de cada valor respecto a la media. $$ \text{Varianza} (s^2) = \frac{\sum (x – \bar{x})^2}{n-1} $$
   • Ejemplo práctico: La varianza en los tiempos de entrega de un servicio puede indicar cuán consistentemente se realizan las entregas.
3. Desviación estándar (s): Es la raíz cuadrada de la varianza y proporciona una medida de la dispersión de los datos en las mismas unidades que los datos originales. $$ s = \sqrt{s^2} $$
   • Significado práctico: La desviación estándar nos indica cuánto varían los valores respecto a la media. Una desviación estándar baja implica que los valores están cerca de la media, mientras que una alta indica una mayor dispersión.

Mediciones de posición relativa

1. Percentiles: Son valores que dividen un conjunto de datos en cien partes iguales. Un percentil indica el valor por debajo del cual se encuentra un cierto porcentaje de los datos.
   • Ejemplo práctico: Si una persona está en el percentil 90 de altura, significa que es más alta que el 90% de las personas de la muestra.
2. Cuartiles: Son valores que dividen un conjunto de datos en cuatro partes iguales.
   • Cuartil 1 (Q1): El 25% de los datos están por debajo de este valor.
   • Cuartil 2 (Q2) o Mediana: El 50% de los datos están por debajo de este valor.
   • Cuartil 3 (Q3): El 75% de los datos están por debajo de este valor.
   • Ejemplo práctico: Los cuartiles pueden usarse para identificar la dispersión y detectar valores atípicos.

3. Datos bivariados

Los datos bivariados son aquellos que incluyen dos variables y nos permiten estudiar la relación entre ellas. Por ejemplo, podríamos analizar la relación entre la altura y el peso de un grupo de personas o entre las horas de estudio y las calificaciones obtenidas por estudiantes.

Gráficas para variables cualitativas

Para datos bivariados con dos variables cualitativas, podemos usar tablas de contingencia y gráficos para visualizar la relación entre las categorías de ambas variables.

1. Tabla de contingencia: Es una tabla que muestra la frecuencia conjunta de dos variables cualitativas. Por ejemplo:

	Categoría B1	Categoría B2	Total
Categoría A1	20	30	50
Categoría A2	10	40	50
Total	30	70	100

2. Gráfico de barras agrupadas: Representa la frecuencia de dos variables cualitativas mediante barras agrupadas, permitiendo comparar categorías de una variable dentro de cada categoría de la otra variable.

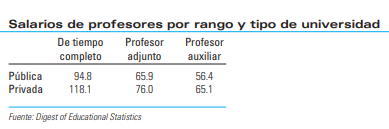
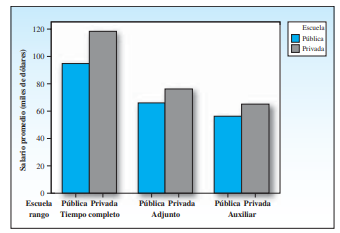
Gráficas de dispersión para dos variables cuantitativas

Para datos bivariados con dos variables cuantitativas, la gráfica de dispersión (scatter plot) es muy útil.

Gráfica de dispersión:

plaintext

Variable Y
|
|
|           ●
|      ●
| ●            ●
|       ●
|          ●
|________________________ Variable X

Cada punto en la gráfica representa una observación con dos valores asociados (X, Y). Esta gráfica nos permite visualizar la relación entre las dos variables cuantitativas y detectar patrones, tendencias o relaciones.

Medidas numéricas para datos cuantitativos bivariados

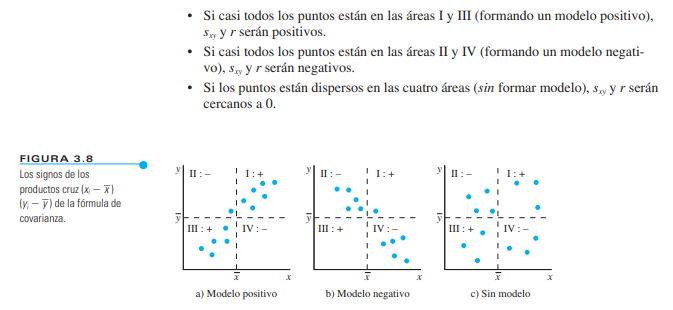
1. Covarianza: Mide el grado de variación conjunta entre dos variables. Si la covarianza es positiva, ambas variables tienden a aumentar juntas. Si es negativa, una variable tiende a aumentar mientras la otra disminuye. $$ \text{Covarianza} (X, Y) = \frac{\sum (x_i – \bar{x})(y_i – \bar{y})}{n-1} $$
   • Ejemplo práctico: La covarianza entre la altura y el peso puede indicar si las personas más altas tienden a pesar más.
2. Coeficiente de correlación de Pearson (r): Mide la fuerza y dirección de la relación lineal entre dos variables. Su valor oscila entre -1 y 1. Un valor de 1 indica una relación positiva perfecta, -1 indica una relación negativa perfecta, y 0 indica que no hay relación lineal. $$ r = \frac{\text{Cov}(X, Y)}{s_X s_Y} $$ Donde sXs_X y sYs_Y son las desviaciones estándar de X e Y respectivamente.
   • Ejemplo práctico: El coeficiente de correlación entre las horas de estudio y las calificaciones puede indicar cuán fuerte es la relación entre ambas.

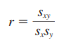
4. Probabilidad y distribuciones de probabilidad

Eventos y el espacio muestral

Evento: En probabilidad, un evento es cualquier resultado o conjunto de resultados posibles de un experimento aleatorio.

Espacio muestral (S): Es el conjunto de todos los posibles resultados de un experimento aleatorio. Cada posible resultado en el espacio muestral se llama «evento elemental».

Ejemplo práctico: Al lanzar un dado, el espacio muestral es S={1,2,3,4,5,6}.

Cálculo de probabilidades con el uso de eventos sencillos

La probabilidad de un evento A se calcula como el número de resultados favorables dividido por el número total de posibles resultados en el espacio muestral.

P(A)=Nuˊmero de resultados favorablesNuˊmero total de resultados en SP(A) = \frac{\text{Número de resultados favorables}}{\text{Número total de resultados en } S}

Ejemplo práctico: Al lanzar un dado, la probabilidad de obtener un 4 es P(4)=16P(4) = \frac{1}{6}.

Relaciones de evento y reglas de probabilidad

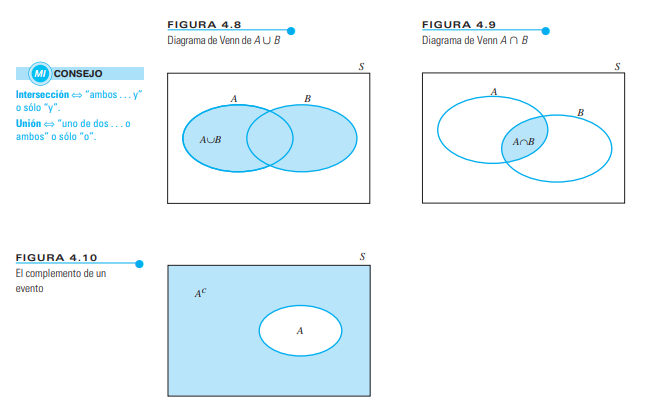
Cálculo de probabilidades para uniones y complementos

Unión de eventos (A∪BA \cup B): La probabilidad de que ocurra al menos uno de los eventos AA o BB.

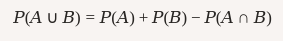
P(A∪B)=P(A)+P(B)−P(A∩B)P(A \cup B) = P(A) + P(B) – P(A \cap B)

Complemento de un evento (AcA^c): La probabilidad de que no ocurra el evento AA.

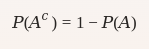
P(Ac)=1−P(A)P(A^c) = 1 – P(A)

Independencia, probabilidad condicional y la regla de la multiplicación

Independencia: Dos eventos AA y BB son independientes si la ocurrencia de uno no afecta la ocurrencia del otro.

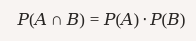
P(A∩B)=P(A)⋅P(B)P(A \cap B) = P(A) \cdot P(B)

Probabilidad condicional: La probabilidad de que ocurra el evento AA dado que ya ocurrió el evento BB.

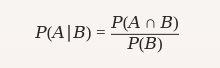
P(A∣B)=P(A∩B)P(B)P(A|B) = \frac{P(A \cap B)}{P(B)}

Regla de la multiplicación: La probabilidad de que ambos eventos AA y BB ocurran.

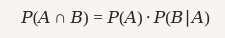
P(A∩B)=P(A)⋅P(B∣A)P(A \cap B) = P(A) \cdot P(B|A)

Regla de Bayes

La regla de Bayes permite calcular la probabilidad condicional de un evento basándose en la probabilidad condicional inversa.

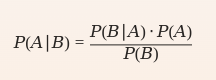
P(A∣B)=P(B∣A)⋅P(A)P(B)P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)}

Variables aleatorias discretas y sus distribuciones de probabilidad

Variables aleatorias: Una variable aleatoria es una función que asigna un valor numérico a cada resultado en el espacio muestral.

Distribuciones de probabilidad

Una distribución de probabilidad asigna una probabilidad a cada valor posible de una variable aleatoria discreta.

Ejemplo práctico: La distribución de probabilidad de lanzar un dado:

Valor (X)	1	2	3	4	5	6
Prob (P)	1/6	1/6	1/6	1/6	1/6	1/6

La media y desviación estándar para una variable aleatoria discreta

Media (Esperanza matemática):

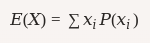
E(X)=∑xiP(xi)E(X) = \sum x_i P(x_i)

Desviación estándar: Medida de la dispersión de los valores de una variable aleatoria respecto a su media.

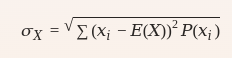
σX=∑(xi−E(X))2P(xi)

Bibliografia

Introducción a la probabilidad y estadística